Audio Source Separation. Unleashing the Power of Non-Negative Matrix Factorization: A Python Implementation.

Have you ever listened to a song and wondered how it's possible to extract individual instruments and vocals from it? Audio source separation is a challenging task that has gained much attention in recent years. It involves separating different sound sources from a mixed audio signal. There are various techniques for audio source separation, but one of the most popular methods is Non-negative matrix factorization (NMF). In this blog post, we will explore how NMF can be used for audio source separation and delve into its underlying mathematical principles. We will also discuss real-life examples and use cases of how NMF is used to extract individual sources from mixed audio signals. So, let's get started!
Non-negative matrix factorization (NMF) has been around for quite some time. It was first introduced in the field of linear algebra in the 1920s, but it was not until the 1990s that it was applied to data analysis and machine learning. In 1999, Daniel D. Lee and H. Sebastian Seung published a groundbreaking paper titled "Learning the parts of objects by non-negative matrix factorization" that popularized the use of NMF for data analysis. Since then, NMF has been used in various applications ranging from image processing to speech recognition. It has become particularly popular in audio source separation, where it is used to extract individual sources from mixed audio signals.
How does Audio Separation with NMF work?
Suppose we have two different sources of audio, for example, a bass guitar, drums and a violin. A single microphone was used to record them, and now we need to separate them to obtain individual tracks for each source.
Before we can separate them, let's understand what mixed audio looks like. Animation 1 shows how two different audio signals become a single signal when recorded using a single microphone.
As you can see, the resulting signal is tricky to understand because it contains information from both sources and the data is very complex. What comes to our help is the Short Time Fourier Transform (STFT), which allows us to extract time-frequency domain data from the mixed signal. This representation is called Spectrogram. This data provides a clearer picture of what the mixed audio looks like.



As we can see from the spectrogram images above, the mixed audio spectrogram contains data from both sources. However, it is evident that the spectrogram exhibits different patterns and structures for each source. This difference in patterns is what makes audio source separation possible using Spectrograms. Now the goal is to find the Spectrogram of the drums and bass guitar track and the violin track having the mixed audio Spectrogram.
The Basic Idea Behind NMF.
NMF, or Non-Negative Matrix Factorization, is a mathematical technique used to decompose a given matrix into two non-negative matrices. The basic idea behind NMF is to find a low-rank approximation of the original matrix by representing it as the product of these non-negative matrices. NMF has been widely used in various fields, including image processing, text mining, and audio source separation. In the context of audio source separation, NMF allows us to separate mixed audio signals into their individual components, enabling us to extract specific sound sources from a mixture. It has proven to be a powerful tool for music production, speech recognition, speech enhancement and audio analysis tasks.
Let's consider a matrix V of size m x n, where m represents the number of rows and n represents the number of columns. NMF aims to find two non-negative matrices W (of size m x r) and H (of size r x n), where r is the desired number of components, such that their product approximates the original matrix V.
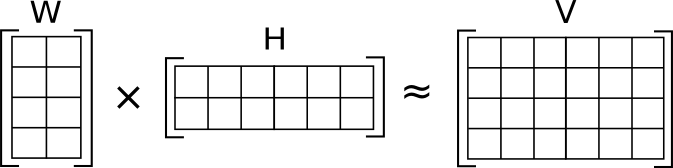
V ≈ WH
In the given example, let's focus on image 4. As shown in the image, the matrix W is approximated by multiplying two matrices: W and H. What's interesting is that the number of columns in W (6 in this case) corresponds to the number of columns in our spectrogram. In this specific scenario, matrix W is decomposed into a matrix with 4 rows and 2 columns. These 2 columns can be thought of as features, which represent certain characteristics or patterns in the audio sources. On the other hand, matrix H has 2 rows and 6 columns, which can be seen as activations or coefficients indicating how strongly each feature is present at each time point or frequency bin. The non-negativity constraint ensures that both W and H consist only of non-negative values, which makes the resulting components additive and meaningful in audio applications.
Now, when we multiply the decomposed matrix W with matrix H, each element in the resulting matrix represents the product of a feature from W and its corresponding activation from H. This multiplication operation is crucial for audio source separation because it allows us to decompose the spectrogram into its constituent features and their activations over time. This decomposition helps us extract specific audio components from a mixture, enabling us to isolate and manipulate individual sources. It's like we're uncovering the underlying structure of the spectrogram and gaining insight into the unique elements that contribute to the mixture.
The task of NMF is to find the optimal values for matrices W and H that minimize the reconstruction error, which is the difference between the original matrix V and its approximation WH. This optimization process can be achieved using various algorithms such as gradient descent or multiplicative updates, which iteratively update the values of W and H until convergence.
Solving NMF Lee and Seung's multiplicative update rule.
Lee and Seung's multiplicative update rule is an iterative algorithm commonly used in Non Negative Matrix Factorization (NMF) to find the optimal values for the matrices W and H. It is based on the principle of minimizing the reconstruction error between the original matrix V and its approximation WH.
The update rule involves iteratively updating the elements of W and H using multiplicative steps. The key idea is to iteratively refine the factorization by updating W and H in a way that reduces the reconstruction error.
For the update rule, we start with randomly initialized non-negative matrices W and H, and then iteratively update their elements until convergence is achieved. Here's how the update equations for W and H look:

In these equations, "*" denotes element-wise multiplication, and "/" refers to element-wise division. The ".T" indicates the transpose of the matrix.
The updates are performed by iteratively estimating the elements of W and H such that the product of W and H approximates the original matrix V, while maintaining non-negativity. The multiplicative nature of these updates helps enforce the non-negativity constraint, ensuring that the resulting W and H matrices consist only of non-negative values.
By repeating the update process, the algorithm aims to minimize the reconstruction error, gradually improving the accuracy of the NMF approximation. The iterations continue until a convergence criterion is met, such as the difference between consecutive reconstructions falls within a predetermined threshold.
Lee and Seung's multiplicative update rule is a computationally efficient method for NMF and has proven to be effective for various applications, including audio source separation, image processing, and topic modeling in text mining.
Python Implementation.
To begin, we need to import certain modules and prepare the audio data. We will utilize torchaudio, a library specifically designed for audio processing tasks, to facilitate this process.
import torch
import torchaudio
from matplotlib import pyplot as plt
from tqdm.notebook import tqdm
x, sr = torchaudio.load("audio.mp3") # Load the audio
x = torchaudio.functional.resample(x, sr, 16000) # Resample to 16000
sr = 16000
Next, we will convert the audio waveform into a spectrogram.
stft = torchaudio.transforms.Spectrogram(n_fft=1024, power=None)(x)
amp = torch.abs(stft) # this is the Spectrogram we want to decompose.
phase = torch.angle(stft)
Now, let's proceed with the main Non-negative Matrix Factorization (NMF) step. In this step, we will perform the NMF algorithm on the previously obtained spectrogram. It is important to note that there are some hyperparameters to consider, and one of them is the choice of the desired number of components, denoted as R. In our case, we will set R to 30, as it has been determined to be an optimal value for our specific scenario. It's worth mentioning that the selection of the right value for R is crucial, as it can impact the quality of the resulting audio source separation. Experimenting with different values of R can help find the optimal configuration that yields the desired separation results.
R = 30
# Randomly initialize the W and H matrices
generator = torch.manual_seed(0)
W = torch.normal(0, 2.5, (rows, R), generator=generator).abs()
H = torch.normal(0, 2.5, (R, cols), generator=generator).abs()
eps = 1e-10
V = amp + eps # We will add epsilon to avoid zeros in our matrix V
MAXITER = 5000
ones = torch.ones(dims)
# We are using GPU acceleration for faster matrix multiplication.
# Skip this line if you do not have GPU.
W, H, V, ones = W.cuda(), H.cuda(), V.cuda(), ones.cuda()
# Iteratively update H and W
for _ in tqdm(range(MAXITER)):
H *= W.T@(V/(W@H))/(W.T@ones)
W *= (V/(W@H))@H.T/([email protected])
# Check the convergence error.
print((W@H - V).mean()) # -2.7256e-09 in our case which is accurate enough.
Now that we have obtained the matrices W and H through NMF, we have a total of 30 features with corresponding time activations. The next step is to separate these features into two distinct groups: one group for bass guitar and drums, and another group for the violin.To achieve this separation, I have manually selected certain features for each group. For the bass guitar and drums group, I have chosen features 0, 2, 4, 6, 7, 16, 18, 19, 27, and 29 from the matrix W. These particular features are believed to represent the spectral patterns or characteristics of the bass guitar and drums.For the violin group, I have assigned the remaining features from the matrix W. These features are considered to capture the spectral patterns specific to the violin. It is worth mentioning that there are various techniques available to filter and assign the features to their respective groups. In this case, I have manually grouped them based on my understanding of the spectral patterns associated with each instrument. Different separation techniques or automated algorithms can also be explored and applied based on the specific requirements and characteristics of the audio sources to achieve an optimal separation quality.
Now, we will create a function that constructs audio for a specific group by combining selected features and their corresponding activation coefficients. This function will allow us to listen to the isolated audio components for each group, providing a clearer understanding of the individual contributions within the original audio mixture.
def separate_source(filters, W, H):
filtered = W[:,filters]@H[filters,:]
reconstructed_amp = filtered * torch.exp(1j*phase)
reconstructed_audio = torchaudio.transforms.InverseSpectrogram(n_fft=1024)(reconstructed_amp)
return reconstructed_audio
To check single source audio just call this function for an index.
audio = separate_source([0], W, H)
Now, lets separate the sources.
# Drums and Bass Guitar
filters = [0, 2, 4, 6, 7, 16, 18, 19, 27, 29]
drums_and_bass = separate_source(filters, W, H)
torchaudio.save('drums_and_base.wav', drums_and_bass.unsqueeze(0), sr)
# Violin
filters = [i for i in range(R) if i not in filters]
violin = separate_source(filters, W, H)
torchaudio.save('violin.wav', violin.unsqueeze(0), sr)
And there is results.
Conclusion.
In conclusion, Non-negative Matrix Factorization (NMF) is a powerful technique for audio source separation and has found applications in various fields. The use of NMF allows us to isolate and extract specific audio components from a mixture, providing valuable insights into the underlying structure of the audio sources.
One of the main advantages of NMF is its ability to work with non-negative data, which aligns well with the nature of audio signals. Additionally, NMF produces additive and interpretable components, making it suitable for tasks like vocals extraction, noise reduction, and remixing. NMF can be implemented efficiently and offers a computationally feasible approach, particularly with algorithms such as Lee and Seung's multiplicative update rule.
However, NMF also has its limitations. One major challenge is the determination of the appropriate number of components (r) to extract. Selecting an incorrect value of r can lead to the loss of important audio information or the inclusion of unnecessary components. NMF is also sensitive to initial conditions and can converge to different solutions, requiring careful tuning and exploration of different parameter settings.
Another limitation is that NMF is a linear model and may struggle with capturing complex relationships or accounting for time-varying characteristics of audio sources.
Despite these limitations, NMF remains a valuable tool for audio source separation and provides a framework for exploring and manipulating audio signals. By considering its strengths and limitations, researchers and practitioners can maximize the potential of NMF in various audio applications and continue to advance the field of audio signal processing.
References
https://wallpaper.dog/digital-art
https://www.nature.com/articles/44565
https://en.wikipedia.org/wiki/Multiplicative_weight_update_methodhttps://en.https://wikipedia.org/wiki/Non-negative_matrix_factorization#:~:text=Non-negative matrix factorization